组合数学中的恒等式
李辰剑 2024-7-23
近日担任《离散数学》助教,批阅期末考卷的时候发现最后一题有许多等价答案,涉及大量组合数的推导与化简。于是我捡起了自高中以后尘封多年的组合数知识,略加推导后整理得出了这篇文章,以供日后参考。同时,也希望这篇文章能帮助到有需要的老师和同学们。
记号约定
本文假设读者有基本的组合数学知识,熟悉组合数 $C_n^k$ 的解析表达式:
组合数/二项式系数有两种主流的记号,除了上述的 $C_n^k$,还有一种表达 $\binom{n}{k}\equiv \C nk$,后一种记号主要用在高等数学和二项式系数中。本文中主要采用前一种记号。
文中不加说明时,参数($m,n,k…$)默认都是自然数。
研究方法:多项式
除了组合数,本文还需要读者熟悉多项式的基本用法。读者也许会有些疑惑,明明是学习组合数学,为什么需要熟悉多项式呢?事实上,组合数与多项式之间有着非常深刻的联系。
考察整幂次的二项式展开:
你会发现,在左边全部展开后(合并同类项之前)得到的的 $2^n$ 个单项式里,恰好有 $\C nk$ 个 $a$ 的幂次为 $k$ 的项,因此等式右边对应的系数刚好就是 $\C nk$。多项式乘法展开后的合并同类项刚好是一次单项式的计数过程。当然,这样的例子还有许多。从多项式出发研究组合数将为我们提供新的视角,而且令许多代数(algebraic)方法成为可能。
多项式和组合数之间有着千丝万缕的联系,而采用多项式研究组合数的方法也将贯穿本文的始终。
第一组恒等式:横向求和
1. 全部横向和
由
我们可以得到:
这是我们的第一个恒等式,我称之为横向全部和。
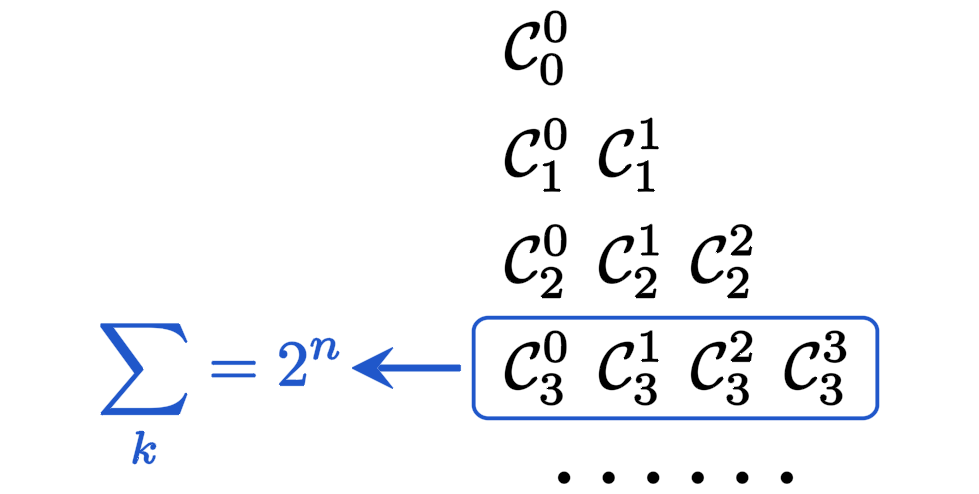
全部横向和在杨辉三角上的示意图

 《戴森球计划》游戏内截图。上:《戴森球计划》中的生产线;下:正在建造中的戴森球。
《戴森球计划》游戏内截图。上:《戴森球计划》中的生产线;下:正在建造中的戴森球。