组合数学中的恒等式

李辰剑 2024-7-23

---

近日担任《离散数学》助教，批阅期末考卷的时候发现最后一题有许多等价答案，涉及大量组合数的推导与化简。于是我捡起了自高中以后尘封多年的组合数知识，略加推导后整理得出了这篇文章，以供日后参考。同时，也希望这篇文章能帮助到有需要的老师和同学们。

记号约定

本文假设读者有基本的组合数学知识，熟悉组合数 $C_n^k$ 的解析表达式：

$$\newcommand\C[2]{C_{ #1}^{ #2}} \C nk\equiv\binom{n}{k}=\frac{n!}{k!(n-k)!}\tag{0.1}$$

组合数/二项式系数有两种主流的记号，除了上述的 $C_n^k$，还有一种表达 $\binom{n}{k}\equiv \C nk$，后一种记号主要用在高等数学和二项式系数中。本文中主要采用前一种记号。

文中不加说明时，参数（$m,n,k…$）默认都是自然数。

研究方法：多项式

除了组合数，本文还需要读者熟悉多项式的基本用法。读者也许会有些疑惑，明明是学习组合数学，为什么需要熟悉多项式呢？事实上，组合数与多项式之间有着非常深刻的联系。

考察整幂次的二项式展开：

$$\newcommand\S[2]{\sum_{ #1=0}^{ #2}} \newcommand\Sn[1]{\sum_{ #1=0}^{n}} \newcommand\Skn{\sum_{k=0}^{n}} \newcommand\Snk\Skn (a+b)^n=\Snk \C nka^kb^{n-k} \tag{0.2}$$

你会发现，在左边全部展开后（合并同类项之前）得到的的 $2^n$ 个单项式里，恰好有 $\C nk$ 个 $a$ 的幂次为 $k$ 的项，因此等式右边对应的系数刚好就是 $\C nk$。多项式乘法展开后的合并同类项刚好是一次单项式的计数过程。当然，这样的例子还有许多。从多项式出发研究组合数将为我们提供新的视角，而且令许多代数（algebraic）方法成为可能。

多项式和组合数之间有着千丝万缕的联系，而采用多项式研究组合数的方法也将贯穿本文的始终。

第一组恒等式：横向求和

1. 全部横向和

由

$$2^n=(1+1)^n=\Snk\C nk \cdot 1^n\cdot 1^{n-k}=\Snk\C nk \notag$$

我们可以得到：

$$\label{eq:sum_C}\tag{1.1} \boxed{\Snk\C nk=2^n}$$

这是我们的第一个恒等式，我称之为横向全部和。

全部横向和在杨辉三角上的示意图

2. 交错和为零/奇偶和相等

类似地，由

$$0=(1-1)^n=\Snk(-)^k\C nk\notag$$

我们可以得到：

$$\boxed{\Snk(-)^k\C nk=0} \tag{1.2}$$

或等价地，表述成奇数项和偶数项和的等式（当$n>0$时）：

$$\label{eq:even_odd} \boxed{\sum_{k\text{ odd}}^{}\C nk=\sum_{k\text{ even}}\C nk} \tag{1.3}$$

即，交错和为零/奇数项=偶数项。

注意到，对于 $n$ 为奇数的情形，利用 $\C nk=\C n {n-k}$ 很容易证明奇偶和相等 $\eqref{eq:even_odd}$；但 $n$ 为偶数的时，必须通过二项式展开才能证明 $\eqref{eq:even_odd}$，其它方法很难证明。

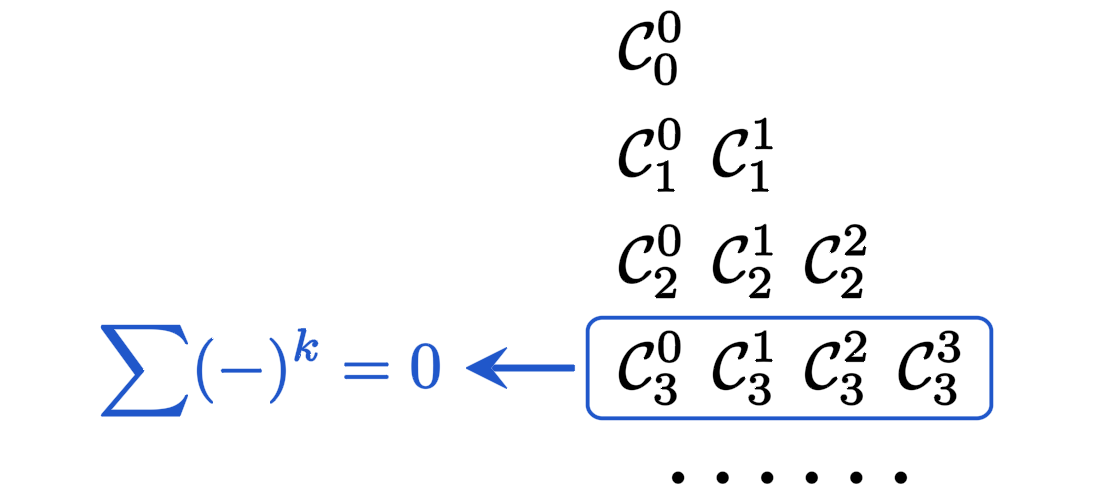
交错和为零在杨辉三角上的示意图

第二组恒等式：杨辉三角

这一组恒等式由杨辉三角中层间的加法关系得到。注意到杨辉三角本身就对应了多项式加法：

$$\begin{align*} (x^2+2x+1)(x+1)&=x^3+2x^2+x\\ &\phantom{=x^3+}+x^2+2x+1\\ &=x^3+3x^2+3x+1\\ &\sim\,[1\quad 2\quad 1]\\ &\qquad\,+[1\quad 2\quad 1]\\ &=[1\quad3\quad3\quad 1] \end{align*}$$

因此这一节的恒等式仍可以看作由多项式导出。

3. 杨辉三角基本关系

$$\label{eq:basic}\tag{2.1} \boxed{\C nk=\C{n-1}{k-1}+\C{n-1}k}$$

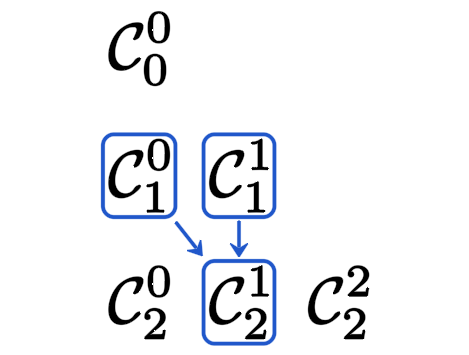
杨辉三角上的基本关系

虽然我们可以从杨辉三角直接“读”出这个恒等式，但是我们也可以通过代数关系硬证，避免“视察法”得到公式的不严谨性。推导如下：

$$\begin{align*} \C{n-1}{k-1}+\C{n-1}k&=\frac{(n-1)!}{(k-1)!(n-k)!}+\frac{(n-1)!}{k!(n-k-1)!}\\ &=\frac{n!}{k!(n-k)!}\cdot\frac kn+\frac{n!}{k!(n-k)!}\cdot\frac{n-k}n\\ &=\frac{n!}{k!(n-k)!}\left(\frac kn+\frac{n-k}n\right)=\C nk\qquad\square. \end{align*}$$

4~5. 裂项与纵向求和

利用二项式定理，组合数的横向求和 $\Snk \C nk=2^n$ 很容易得到；但是纵向求和 $\sum_{m=0}^n\C{m}k$ 就不那么 trivial 了。

逆用上面的基础关系 $\eqref{eq:basic}$，可以给出组合数的裂项 $\C{n-1}{k-1}=\C nk-\C{n-1}k$，即

$$\boxed{\C nk=\C{n+1}{k+1}-\C n{k+1}} \tag{2.2}\label{eq:break_into_two}$$

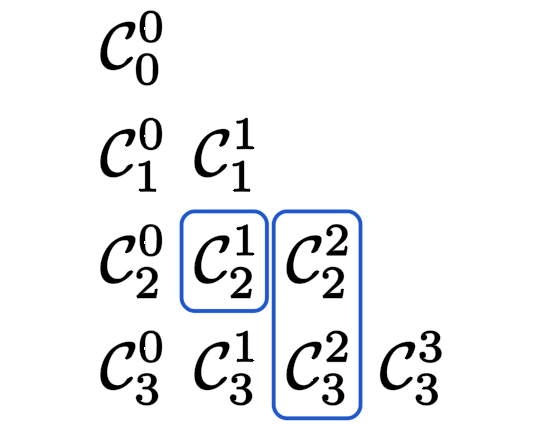
杨辉三角上的组合数裂项

对 $n$ 求和，即有：

$$\begin{align*} \Sn{m}\C m k&=\Sn m \C{m+1}{k+1}-\C m{k+1}\\ &=\C{n+1}{k+1}-\C0{k+1} \end{align*}$$

$\C0{k+1}$ 是什么？严谨细心的同学固然会觉得上面的推导搞错了边界条件；但另一种更为霸道取巧的方法是补充定义 $n\ge k$ 的 $\C nk$，让记号顺着数学走。

$\C nk$ 的拓展定义

定义 当 $k>n$ 时，补充定义 $\C nk=0$。即：

$$\C nk=\left\{\begin{array}l \frac{n!}{k!(n-k)!} & k\le n \\ 0 & k>n, \end{array}\right. \quad \text {for } k,n\in\mathbb N. \tag{2.5}\label{eq:generalization1}$$

不难发现，此时递推关系 $\C nk=\C{n-1}{k-1}+\C{n-1}k$ 仍成立；因此裂项 $\eqref{eq:break_into_two}$ 仍成立。

在一些涉及代数的问题中，也会给出另一种对 $\C nk$ 的推广：

$$\binom{\nu}{k}:=\frac{\nu(\nu-1)\cdots(\nu-k+1)}{k!},\quad \text{for }\nu\in\mathbb R,k\in\mathbb N. \label{eq:generalization2}\tag{2.6}$$

这种推广来自于拓展的二项式定理，分子的形式类似多项式求导的系数，更适合泰勒展开。那么，这两种推广是否兼容呢？案是肯定的。当 $n<k$ 时，代数推广 $\eqref{eq:generalization2}$ 变为：

$$\C nk\overset{\eqref{eq:generalization2}}{=}\frac{n\cdot(n-1)\overbrace{\cdots}^{\text{有一项为0}}(n-k+1)}{k!}=0\notag$$

与 $\eqref{eq:generalization1}$ 相符。

5. 纵向求和

回到前面。根据我们的推广有 $\C 0{k+1}=0$，于是我们得到组合数的纵向求和公式：

$$\boxed{\Sn{m}\C m k=\C{n+1}{k+1}} \label{eq:n_sum}\tag{2.3}$$

这是杨辉三角中一整列组合数的求和；根据裂项公式（或者逆用 $\eqref{eq:n_sum}$）我们还可以给出另一个推论，即部分的纵向求和：

$$\boxed{\sum_{m=a}^b\C m k=\C{b+1}{k+1}-\C{a}{k+1}} \label{eq:partial_n_sum}\tag{2.4}$$

其中 $a,b\in\mathbb N$ 分别是下标求和的下限和上限（即有 $a<b$）。

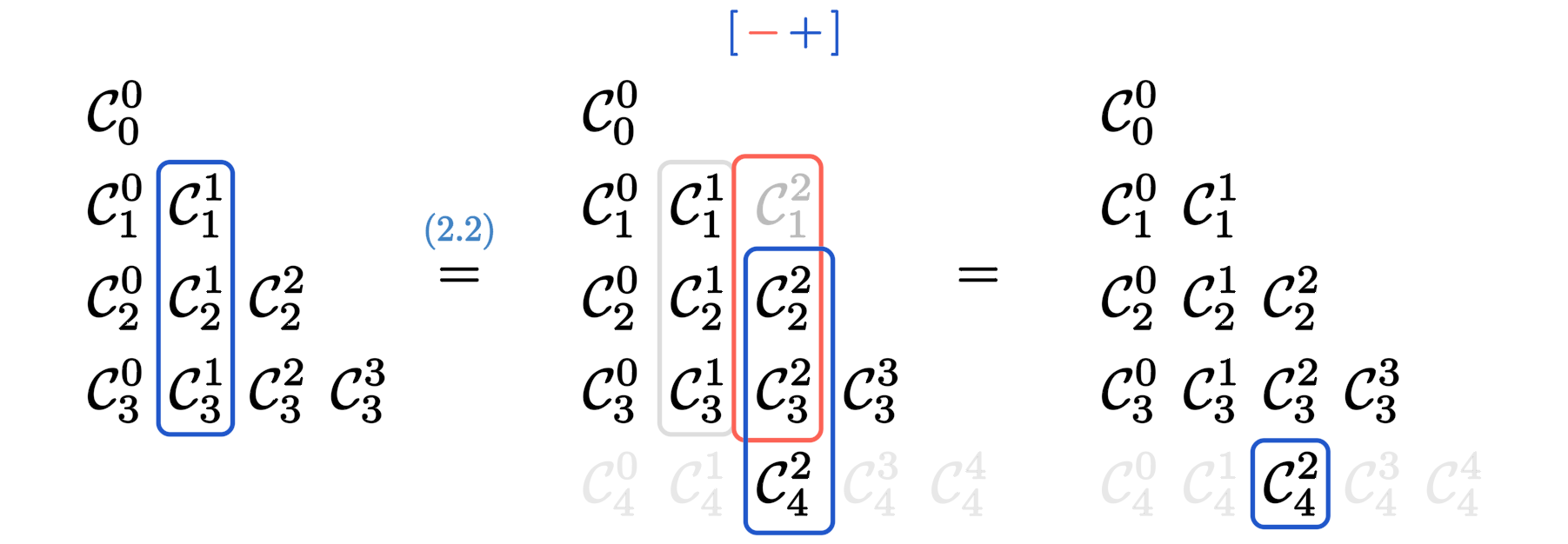
杨辉三角上证明纵向求和公式

例题：广义球盒问题

学数学如果只学定义和定理，便味同嚼蜡，如同纸上谈兵。即使一日千里，也无法真正理解其中的数学。只有通过 nontrivial 问题的磨砺，才能帮助我们窥探到数学理论的深层含义，帮助我们加深对数学工具的理解、认识到数学工具的真正边界。

在这里，我给出一道经典的球盒计数问题，并用经典的排列组合方法和生成函数两种方法分别给出答案。我们将会看到，为了证明两种方法给出的答案相等，必须灵活、综合地运用前述的排列组合恒等式；它们在推导中将起到无可替代的作用。

例题 将 $n$ 个不可区分的小球放入编号为 $1,2,\cdots,m$ 的盒（即 $m$ 个可区分的盒）中，分别对以下几种情况求方法数。

(1) 没有限制；
(2) 第一个盒有 $k$ 个球时；
(3) 第一个盒有不超过 $k$ 个球；
(4) 对于 $i=1,2,3$ 均有第 $i$ 号盒子中球的个数不等于 $i$，这里 $m\ge4,n\ge6$。

解答 (1) $\langle方法一\rangle$ 插板法

假象所有的 $n$ 个球排成一列，将 $m$ 个盒子想象为 $m-1$ 个分隔板，只需要在 $n$ 个球中插入所有分隔板即可。所有的 $n$ 个球和 $m-1$ 个分隔板放成一列，一共有 $n+(m-1)$ 个位置，只需在其中 $m-1$ 个位置放入分隔板即可。因此一共有 ${\rm ans}(n,m)=\C{n+m-1}{m-1}=\C{n+m-1}{n}$ 种方法。

插板法解球盒问题示意图

将 $n$ 个不可区分球放入 $m$ 个可区分盒的放法数量记为 $\mathrm{bib}(n,m)=\C{n+m-1}{m-1}=\C{n+m-1}{n}$。

bib = ball in box

$\langle方法二\rangle$ 生成函数

$n$ 个球放入 $m$ 个盒，只需要计算 $n_1+n_2+\cdots n_m=n$ 的自然数解的数量即可。这刚好对应了多项式

$$\newcommand\bib{ {\rm bib}} \newcommand\coef{ {\rm coef}} \underbrace{(1+x+x^2+\cdots)(1+x+x^2+\cdots)\cdots(1+x+x^2+\cdots)}_{共m项}\notag$$

展开后 $x^n$ 的系数。因此，我们只需要计算

$$F(x)=(1+x+x^2+\cdots)^m=\frac{1}{(1-x)^m}\notag$$

的展开式中 $x^n$ 项的系数即可。$F(x)$ 被称为问题的生成函数。

生成函数又是一个大坑。生成函数在数列、组合数学、离散数学、特殊函数、概率论等领域都有重要的应用。
也许以后能再开笔记专门讨论生成函数；这里就不展开了。

记多项式 $f(x)$ 中 $x^n$ 项的系数为 $\coef_n F(x)$。根据广义的二项式定理（或者，二项式的泰勒展开），则有：

$$F(x)=(1-x)^{-m}=\sum_{k=0}^{+\infty}\binom{-m}{k}(-x)^k\notag$$

即 $\coef_k F(x)=(-)^k\cdot\binom{-m}{k}$。这里的系数可以由泰勒展开得到：

$$\begin{align*} \binom{-m}{k}&=\frac{(-m)(-m-1)\cdots(-m-k+1)}{k!}\\ &=(-)^k\frac{m(m+1)\cdots(m+k-1)}{k!}=(-)^k\C{m+k-1}{k} \end{align*}$$

因此答案就是 $(-)^k\cdot\left.\binom{-m}{k}\right|_{k=n}=\C{m+n-1}{n}$，与 $\langle方法一\rangle$ 得到的结果是一样的。

(2) 第一个盒有 $k$ 个球，则问题退化为 $n-k$ 个球装入 $m-1$ 个盒的情形。答案为：

$$\bib(n-k,m-1)=\C{n+m-k-2}{n}\notag$$

(3) $\langle方法一\rangle$ 生成函数

注意到此时第一个盒子里最多只能有 $k$ 个球，这对应了多项式的幂次不超过 $k$。对应的生成函数为：

$$\begin{align*} F(x)&=(1+x\cdots x^k)(1+x+\cdots)^{m-1}\\ &=\frac{1-x^{k+1}}{1-x}\cdot \frac{1}{(1-x)^m}\\ &=\frac{1-x^{k+1}}{(1-x)^m} \end{align*}$$

而 $F(x)$（的展开式中）$x^n$ 的系数即为问题的答案。

注意到 $\coef_n \{x^k F(x)\}=\coef_{n-k}F(x)$，我们得到：

$$\begin{align*} {\rm ans}&=\coef_n F(x)\\ &=\coef_n\left\{\frac{1-x^{k+1}}{(1-x)^m}\right\}\\ &=\coef_n\{(1-x)^{-m}\}-\coef_n\{x^{k+1}(1-x)^{-m}\}\\ &=\C{n+m-1}{m-1}-\C{n+m-k-2}{m-1} \end{align*}$$

$\langle方法二\rangle$ 组合数学

生成函数法给出了非常漂亮的结论；那么组合数学方法能否给出答案呢？答案是肯定的。

从组合数学的视角，盒一中装有不超过 $k$ 个球，可以分为没有球、装有 $1$ 个球、…、装有 $k$ 个球这 $k+1$ 种情况。利用(2)的结论，可以得到答案：

$$\sum_{i=0}^k \bib(n-i,m-1)=\sum_{i=0}^{k}\C{n+m-i-2}{m-2}\notag$$

计算并不复杂；但是问题在于，如何验证两种方法给出的答案相等呢？这时我们可以利用组合数的纵向求和公式 $\eqref{eq:partial_n_sum}$ 化简上式：

$$\sum_{i=0}^k\C{n+m-i-2}{m-2}\overset{\eqref{eq:partial_n_sum}}{=}\C{n+m-1}{m-1}-\C{n+m-k-2}{m-1}\notag$$

终于得到了相同的答案。

(4) 终于到了最难的最后一小问。这里我们同样有两种选择，走组合数学的老路，或者诉诸生成函数。前期计算并不困难，只是有些繁琐；但最后的化简并不容易。这里，我们还是把组合数学的方法放在前面。

$\langle方法一\rangle$ 广义容斥原理|组合数学

解用概率论中的记号，记事件 $P_i=「盒i中球数=i」$，$\#(P)$ 表示满足事件 $P$ 的不同放法的数量。则题目所求数字可表示为 $\#(\overline P_1\overline P_2\overline P_3)$，其中 $\overline P$ 表示事件的反。根据广义容斥原理，我们可以得到：

$$\#(\overline P_1\overline P_2\overline P_3)=\#(\varnothing)-\sum_i\#P_i+\sum_{i\neq j}\#P_iP_j-\#P_1P_2P_3\notag$$

根据前面几小问的经验，不难得出

$$\begin{align*} \#:=\#(\varnothing)&=\C{n+m-1}{n}\\ \#(P_i)&=\C{n+m-i-2}{n-i}=\C{n+m-i-2}{m-2}\\ \#(P_iP_j)&=\C{n+m-i-j-3}{m-3}\\ \#(P_iP_jP_k)&=\C{n+m-i-j-k-4}{m-4} \end{align*}$$

带入上式，即可得到：

$$\begin{align*} {\rm ans}&=\#(\varnothing)-\sum_i\#P_i+\sum_{i\neq j}\#P_iP_j-\#P_1P_2P_3\\ &=\C{n+m-1}{m-1}-\sum_i\C{n+m-i-2}{m-2}+\sum_{i\neq j}\C{n+m-i-j-3}{m-3}-\C{n+m-i-j-k-4}{m-4}\big|_{i,j,k=1,2,3}\\ &=\underbrace{\C{n+m-1}{m-1}-\sum_{i=1}^3\C{n+m-i-2}{m-2}+\sum_{i=3}^5\C{n+m-i-3}{m-3}-\C{n+m-10}{m-4}}_{共8项} \end{align*}$$

大多数同学做到这里便以为结束了，收工大吉。但实际上这个结果可以进一步化简。首先利用纵向求和，再观察到杨辉三角上相邻位置的邻组合数进行化简，最终可以化简为只有 4 项的结果。

$$\begin{align*} &&\phantom{++++++}&\underbrace{ \C{n+m-1}{m-1}- \color{blue}{\sum_{i=1}^3\C{n+m-i-2}{m-2}}+ \color{blue}{\sum_{i=3}^5\C{n+m-i-3}{m-3}}- \C{n+m-10}{m-4} }_{共8项}\\ &&\overset{\color{grey}{\sum_{p}\C p k=\C{p+1}{k+1}}\phantom{+..}}{=}& \C{n+m-1}{m-1}- \color{blue}{\big(\C{n+m-2}{m-1}-\C{n+m-5}{m-1}\big)}+ \color{blue}{\big(\C{n+m-5}{m-2}-\C{n+m-8}{m-2}\big)}- \C{n+m-10}{m-4}\\ &&=\overset{\phantom{===.}}{}& \color{magenta}{\big(\C{n+m-1}{m-1}-\C{n+m-2}{m-1}\big)}+ \color{magenta}{\big(\C{n+m-5}{m-1}+\C{n+m-5}{m-2}\big)} -\C{n+m-8}{m-2}-\C{n+m-10}{m-4}\\ &&\overset{\color{grey}{\C nk=\C{n-1}{k-1}+\C{n-1}k}}{=}&\underbrace{ \color{magenta}{\C{n+m-2}{m-2}}+ \color{magenta}{\C{n+m-4}{m-1}}- \C{n+m-8}{m-2}-\C{n+m-10}{m-4}}_{共4项} \end{align*}$$

这样我们就得到了最简的结果：只有四项，且每项系数绝对值都为 1。我们可以用「不同项之间是否在杨辉三角中相邻」来衡量是否还有进一步化简的空间：任何项在杨辉三角中都不相邻，前述恒等式都无法直接触发，大概率无法进一步化简。

$\langle方法二\rangle$ 生成函数

这一小问用生成函数1同样可以求解。而且相比广义容斥原理迂回曲折的计算过程，生成函数更为直接清晰。然而我们将会看到，“复杂性不会消失，只会转移”；作为更清晰的数学图像的代价，生成函数法的计算和化简更为复杂，除非铺开草稿纸仔细演算，否则在压力下几乎不可能算出最终的最简结果。

我们前面提到，计算球盒问题的方法数，等价于计算如下多项式

$$\underbrace{(1+x+x^2+\cdots)(1+x+x^2+\cdots)\cdots(1+x+x^2+\cdots)}_{共m项}\notag$$

中 $x^n$ 项的系数。于是，计算第 $i$ 个盒子中球数 $\neq i(i=1,2,3)$ 的情况数量，只需要在前三个盒子（前三个因子）中分别禁止 $x,x^2,x^3$ 即可。于是我们得到对应的生成函数：

$$\begin{align*} F(x)&=(1+x^2+x^3\cdots)(1+x+x^3\cdots)(1+x+x^2+x^4\cdots)\cdot(1+x+x^2+\cdots)^{m-3}\\ &=\left(\frac{1}{1-x}-x\right)\left(\frac{1}{1-x}-x^2\right)\left(\frac{1}{1-x}-x^3\right)\cdot\left(\frac{1}{1-x}\right)^{m-3}\\ &=(1-x+x^2)(1-x^2+x^3)(1-x^3+x^4)\cdot\frac{1}{(1-x)^m} \end{align*}$$

这里我们遇到了生成函数法的第一个难点：如何展开并化简前面的多项式？直接展开共有 3x3x3=27 项，极易出错。解决方案是分组展开、竖式合并。

$$\begin{align*} &\phantom{+}(1-x+x^2)(1-x^2+x^3)(1-x^3+x^4)\\ &=\big[1-x(1-x)\big]\big[1-x^2(1-x)\big]\big[1-x^3(1-x)\big]\\ &=1\color{blue}{-(x+x^2+x^3)(1-x)}\\ &\phantom{++}\color{magenta}{+(x^3+x^4+x^5)(1-x)^2}-x^6(1-x)^3\\ &=1\color{blue}{-x-x^2-x^3}\\ &\phantom{++++}\color{blue}{+x^2+x^3+x^4}\\ &\phantom{++++++.}\color{magenta}{+x^3+x^4+x^5}\\ &\phantom{++++++++}\color{magenta}{-2x^4-2x^5-2x^6}\\ &\phantom{+++++++++++}\color{magenta}{+x^5+\ \ x^6+x^7}\\ &\phantom{+++++++++++++.}-x^6+3x^7-3x^8+x^9\\ &=1-x\phantom{++..}+x^3\phantom{++++..}-2x^6+4x^7-3x^8+x^9\\ &=1-x+x^3-2x^6+4x^7-3x^8+x^9 \end{align*}$$

有了这个结果之后，后面的步骤并不困难，我们很快就能写出答案。记 $\frac{1}{(1-x)^m}$ 展开式中 $x^n$ 项系数为 $\C{n-m-1}{m-1}=:c_n$，则

$$\begin{align*} {\rm ans}&=c_n-c_{n-1}+c_{n-3}-2c_{n-6}+4c_{n-7}-3c_{n-8}+c_{n-9}\\ &=\C{n-m-1}{m-1}-\C{n-m-2}{m-1}+\C{n-m-4}{m-1}-2\C{n-m-7}{m-1}+4\C{n-m-8}{m-1}-3\C{n-m-9}{m-1}+\C{n-m-10}{m-1} \end{align*}$$

接下来我们就遇到了生成函数法的第二个难点：如何化简。根据 $\langle方法一\rangle$ 的结果，我们知道上式应该可以化简成只有四项的答案；但如今不仅项数多（仍有七项），而且系数也不规律。真的能化简吗？

答案是肯定的。实际上，只需要注意观察系数、有方向的凑配即可。真正用到的恒等式只有最简单的杨辉三角基本关系 $\eqref{eq:basic}$。

$$\newcommand\CC[2]{\C{n-m-#1}{m-#2}} \begin{align*} {\rm ans}&=\color{blue}{\CC11-\CC21}+\CC41-2\CC71+4\CC81-3\CC91+\CC{10}1\\ &=\color{blue}{\CC22}+\CC41-\color{blue}{2\big(\CC71-\CC81\big)}+\color{blue}{2\big(\CC81-\CC91\big)}-\color{blue}{\big(\CC91-\CC{10}1\big)}\\ &=\CC22+\CC41-\color{blue}{2\CC82}+\color{blue}{2\CC92}-\color{blue}{\CC{10}2}\\ &=\CC22+\CC41-\color{magenta}{\big(\CC82-\CC92\big)}-\CC82+\color{magenta}{\big(\CC92-\CC{10}2\big)}\\ &=\CC22+\CC41-\color{magenta}{\CC93+\CC{10}3}-\CC82\\ &=\CC22+\CC41-\CC82-\color{magenta}{\CC{10}4} \end{align*}$$

其中，用颜色标出来的地方便是应用基本关系的项。至此，我们终于得到了最简结果，这一结果也与 $\langle方法一\rangle$ 中结果相符。

第三组恒等式：求导

6. 带一次项的组合数求和

我们先给出恒等式，然后再给出推导。

$$\boxed{\Snk k\C nk=n2^{n-1}}\tag{3.1}$$

乍一看，$k\C nk$ 求和与以往的任何的组合数求和形式都不同，仿佛无从下手；但请读者记住，形如 $kx^k$ 的求和往往和求导有关，因为只有求导会从 $x^k$ 上拉一个 $k$ 下来，而计算 $\sum x^k$ 就简单多了。因此，我们考虑利用求导来证明上式。

在二项展开 $(1+x)^n=\Snk \C nk x^k$ 两边作用 $\frac{\mathrm d}{\mathrm dx}$，得到：

$$n(1+x)^{n-1}=\S nk k\C nk x^{k-1}\notag$$

令 $x=1$，即可得到上式。

利用类似方法，多次求导后还可以得出

$$\S nk k^2\C nk=n(n+1)2^{n-2}\notag$$

等更多恒等式。这里就不展开赘述了。

第四组恒等式：卷积

7. 积之和/卷积公式

我们同样先给出恒等式，然后再给出推导。

$$\boxed{\sum_{k=0}^r\C mk\C n{r-k}=\C{m+n}r} \label{eq:convol}\tag{4.1}$$

其中 $r\le\min\{m,n\}$。乍一看，之前的恒等式都是单项组合数的组合；这里是两项组合数乘积的求和，如何处理？理解这个恒等式的关键，在于注意到反向（$k$ 与 $r-k$）相乘这个类似卷积的结构。于是我们可以构造多项式的“卷积”，从多项式乘法中提取出上述等式。考虑

$$\left(\sum_{k=0}^m\C mk x^k\right)\left(\sum_{k'=0}^n\C n{k'} x^{k'}\right)\notag$$

则其展开式中 $x^r$ 的系数为

$$\begin{align*} \boxed{\cdots}x^r&=\C m0x^0\cdot\C nr x^r+\C m1 x^1\cdot\C n{r-1}x^{r-1}+\cdots\\ &=\left(\sum_{k=0}^r\C mk\C n{r-k}\right)\cdot x^k \end{align*}$$

另一边，又有

$$\begin{align*} &\phantom{=}\left(\sum_{k=0}^m\C mk x^k\right)\left(\sum_{k'=0}^n\C n{k'} x^{k'}\right)\\ &=(1+x)^m\cdot(1+x)^n=(1+x)^{m+n} \end{align*}$$

根据二项式定理，其中 $x^r$ 项系数为 $\C{m+n}r$。于是我们得到

$$\sum_{k=0}^r\C nk\C n{r-k}=\C{m+n}r\quad \square.\notag$$

实际上，使用向量记号，我们可以把 $\eqref{eq:convol}$ 表示成真正的卷积形式：

$${\vec C}_{m+n}=\vec C_m* \vec C_n\notag$$

其中 $\vec C_n:=(\C n0,\C n1,\cdots,\C nn)$ 表示一个组合数构成的向量，$*$ 表示向量间的卷积运算。

由 $\eqref{eq:convol}$，我们还可以得到两个推论：

推论 1 令 $m=n$，我们有

$$\sum_{k=0}^r\C nk\C n{r-k}=\C{2n}r\notag$$

推论 2 利用 $\C nk = \C n{n-k}$，有

$$\sum_k\C mk\C nk = \sum_k\C nk \C n{n-k}=(\vec C_{m+n})_n=\C{m+n}n\notag$$

因此得到

$$\sum_{k=0}^{\min\{m,n\}}\C mk \C nk=\C{m+n}n\notag$$

推论 3 回顾杨辉三角的基本关系，基本关系 $\C nk=\C{n-1}{k-1}+\C{n-1}k$ 其实是卷积公式 $\eqref{eq:convol}$ 的一种特殊情况。这是因为基本关系来自于杨辉三角，杨辉三角的构造方法本质上来源于多项式相乘，而多项式相乘又蕴含了卷积。

$$\begin{align*} (x+1)(x+1)&=x^2+x\\ &\phantom{++..}+x+1\\ &=x^2+2x^2+1\\ &\sim\,[1\quad 1]\\ &\qquad\,+[1\quad 1]\\ &=[1\quad2\quad 1] \end{align*}$$

具体来说，在卷积公式 $\eqref{eq:convol}$ 中令 $m=1$，$r=k$，将原本的求和哑变量用 $\ell$ 替代，则有

$$\sum_{\ell=0}^1\C 1\ell\C n{k-\ell}=\C{n+1}k\\ \implies 1\cdot \C nk+1\cdot \C n{k-1}=\C{n+1}k\\ \implies \C nk+\C{n}{k-1}=\C{n+1}k\notag$$

再令 $k\to k+1$，就得到了 $\C nk+\C n{k+1}=\C{n+1}{k+1}$，即基本关系。

总结

从头至尾，从多项式展开、到基于多项式卷积的杨辉三角，再到多项式求导，可以说所有的组合数恒等式背后都有着多项式的影子。这些组合数学恒等式用定义直接证明往往非常复杂，if not impossible；对于难以使用组合数定义直接证明的恒等式，另一种方法是采用归纳法证明，但是数学归纳法只管证明，却很难展示出等式背后的数学含义和背景。而一旦从多项式出发，困难则迎刃而解，而且往往能很好地揭示看出恒等式背后的数学根源。可以说，组合数学恒等式的赞歌，便是一曲多项式的赞歌。

事实上，多项式对组合数学的贡献并不止步于此。数学家们不满足于用多项式仅仅来证明几个恒等式，随后又发明了生成函数，找到了将多项式直接应用于组合数学的方法。简单来说，数一个多项式展开式中某个 $x^n$ 项的数量（即 $x^n$ 项的系数），就刚好对应了「多项式的各个因子乘起来，有多少种组合方式能得到 $x^n$」，从而可以对应许多 nontrivial 组合计数问题的答案。这一方法不仅仅是将组合数学问题 encode 到多项式中那么简单，它更意味着我们可以利用多项式的丰富的代数性质来进行运算，例如求导、泰勒展开等等。多项式本为代数（algebraic）对象，但通过 exploit（有意或刻意地利用）其算数（arithmetic）性质，数学家得以极大的扩展组合数学的计算方法。可以说，组合数学的赞歌，是一曲多项式的赞歌。

生成函数又是一个大坑。除了组合数学，生成函数在数列、特殊函数、概率论等领域都有不亚于组合数学中重要性的应用。

也许以后能再开笔记专门讨论生成函数；这里就不展开了。

最后，我将各个恒等式的背景和它们之间的关系梳理成图，以供参考。

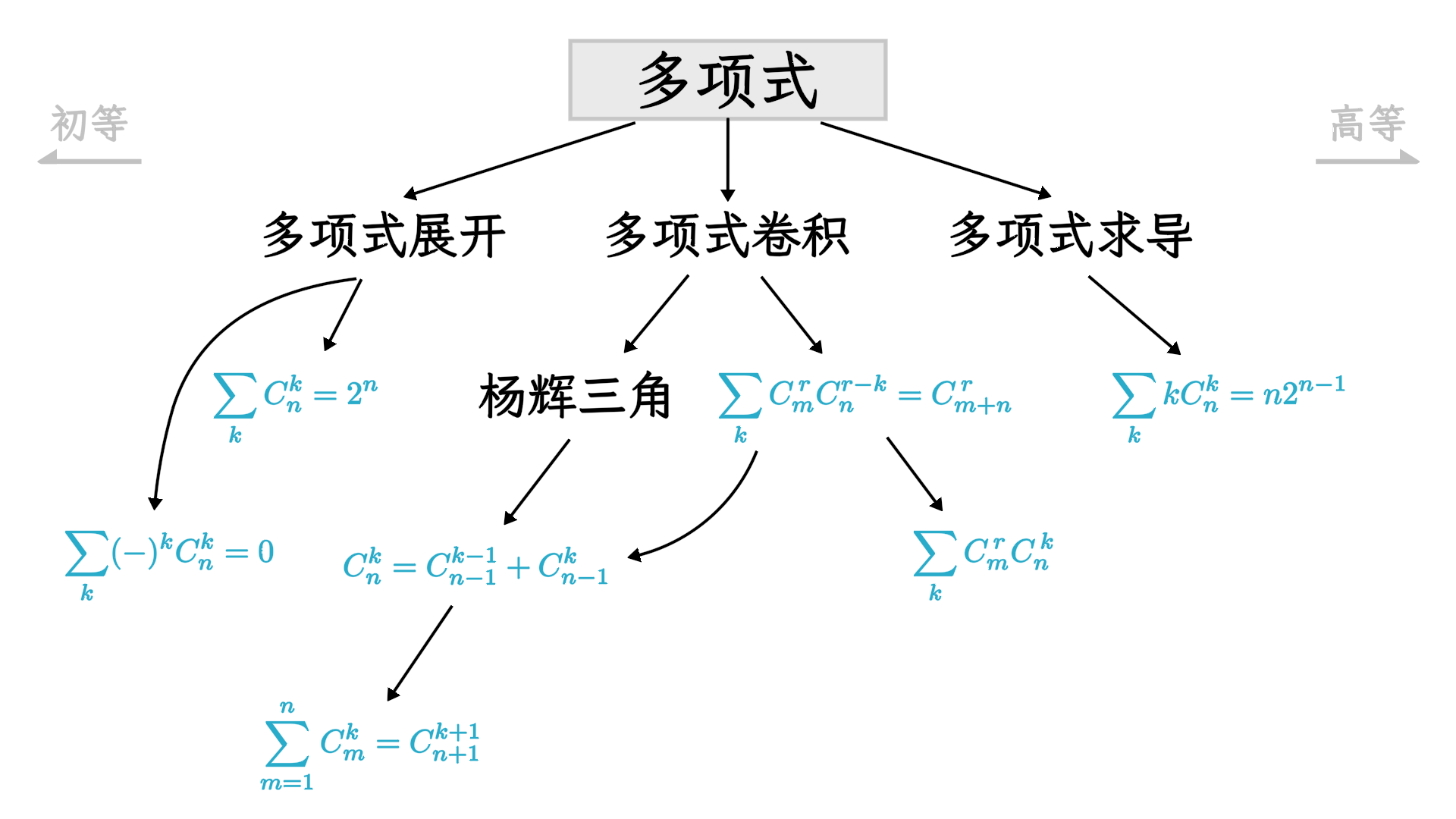
组合数恒等式间的关系

参考文献

本文中选取的部分恒等式参考了如下文章。

[1] 【组合数学】组合恒等式总结 ( 十一个组合恒等式 | 组合恒等式证明方法 | 求和方法 ) ★，by 韩曙亮，2020 年发布于 CSDN，https://blog.csdn.net/shulianghan/article/details/109180924.